From Highly Structured E-Infinity Rings and Transfinite Maximally Symmetric Manifolds to the Dark Energy Density of the Cosmos

From Highly Structured E-Infinity Rings and Transfinite Maximally Symmetric Manifolds to the Dark Energy Density of the Cosmos

From Highly Structured E-Infinity Rings and Transfinite Maximally Symmetric Manifolds to the Dark Energy Density of the Cosmos

 Download as PDF (Size:2562KB)  HTML   XML  PP. 641-648  

DOI: 10.4236/apm.2014.412073    695 Downloads   849 Views  

Author(s)    Leave a comment

Mohamed S. El Naschie^1*

Affiliation(s)

¹Department of Physics, University of Alexandria, Alexandria, Egypt.

ABSTRACT

Starting from well established results in pure mathematics, mainly transfinite set theory, E-infinity algebra over operads, fuzzy manifolds and fuzzy Lie symmetry groups, we construct an exact Weyl scaling for the highly structured E-infinity rings corresponding to E-infinity theory of high energy physics. The final result is an exact expression for the energy density of the cosmos which agrees with previous analysis as well as accurate cosmological measurements and observations, such as COBE, WMAP and Planck. The paper is partially intended as a vivid demonstration of the power of pure mathematics in physics and cosmology.

KEYWORDS

Highly Structured Rings, E-Infinity, Loop Spaces, High Energy Physics, Dark Energy, Einstein Relativity, Fractal-Cantorian Spacetime, Nonlinear Dynamics, Quantum Chaos

Cite this paper

Naschie, M. (2014) From Highly Structured E-Infinity Rings and Transfinite Maximally Symmetric Manifolds to the Dark Energy Density of the Cosmos. Advances in Pure Mathematics, 4, 641-648. doi:10.4236/apm.2014.412073.

References

[1]	Weibel, P., Ord, G. and Rossler, O., Eds. (2005) Spacetime Physics and Fractality. Festschrift in Honour of Mohamed El Naschie on the Occasion of His 60th Birthday. Springer, Vienna-New York.
[2]	Yang, C.N. (1987) Square Root of Minus One, Complex Phases and Erwin Schrodinger. In: Kilmister, C.W., Ed., Schrodinger—Centenary Celebration of a Polymath, Cambridge University Press, Cambridge, UK, 53-64.
[3]	Donaldson, S.K. and Kronheimer, P.B. (1990) The Geometry of Four Manifolds. Oxford University Press, Oxford.
[4]	Kodiyalam, V. and Sunder, V.S. (2001) Topological Quantum Field Theories from Subfactors. Chapma & Hall/Crc, London, UK.
[5]	'tHooft, G. (2005) 50 Years of Yang-Mills Theory. World Scientific, Singapore. http://dx.doi.org/10.1142/5601
[6]	El Naschie, M.S., Rossler, O.E. and Prigogine, I. (1995) Quantum Mechanics, Diffusion and Chaotic Fractals. Pergamon Press/Elsevier, Oxford.
[7]	He, J.-H. (2005) Transfinite Physics. China Scientific and Culture Publishing, Shanghai.
[8]	Sidharth, B.G. and Altaisky, M.V. (2001) Frontiers of Fundamental Physics. Kluwer Academic/Plenum Publishers, New York (see in particular 81-95).
[9]	Friedlander, E. and Grayson, D. (2005) Handbook of K-Theory. Springer, Berlin. http://dx.doi.org/10.1007/978-3-540-27855-9
[10]	Cartier, P., Julia, B., Moussa, P. and Vanhove, P. (2006) Frontiers in Number Theory, Physics and Geometry I. Springer, Berlin.
[11]	El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
[12]	E-Infinity Group: E-Infinity High Energy Communication Nos. 1 to 90. E-Infinity Energyblogspot.com.
[13]	Baker, A. (2013) Close Encounters of the E-Infinity Kind. Journal of Homotopy and Related Structures, 9, 257-282.
[14]	El Naschie, M.S. (1995) Banach-Tarski Theorem and Cantorian Spacetime. Chaos, Solitons & Fractals, 5, 1503-1508. http://dx.doi.org/10.1016/0960-0779(95)00052-6
[15]	El Naschie, M.S. (2011) Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53. http://dx.doi.org/10.4236/jqis.2011.12007
[16]	Yau, S.-T. (2010) The Shape of Inner Space. Basic Book—Perseus Book Group, New York.
[17]	El Naschie, M.S. (1997) Advanced Prerequisites for E-Infinity Theory. Chaos, Solitons & Fractals, 30, 636-641.
[18]	Argyris, J. and Ciubotariu, C. (1997) On El Naschie’s Complex Time and Gravitation. Chaos, Solitons & Fractals, 8, 743-751. http://dx.doi.org/10.1016/S0960-0779(97)00072-6
[19]	Sigalotti, L. and Mejias, A. (2006) The Golden Ratio in Special Relativity. Chaos, Solitons & Fractals, 30, 521-524. http://dx.doi.org/10.1016/j.chaos.2006.03.005
[20]	El Naschie, M.S. (1994) On Certain “Empty” Cantor Sets and Their Dimensions. Chaos, Solitons & Fractals, 4, 293-296. http://dx.doi.org/10.1016/0960-0779(94)90152-X
[21]	Crasmareanu, M. and Hretcanu, C. (2008) Golden Differential Geometry. Chaos, Solitons & Fractals, 38, 1229-1238. http://dx.doi.org/10.1016/j.chaos.2008.04.007
[22]	El Naschie, M.S. (1998) Von Neumann Geometry and E-Infinity Quantum Spacetime. Chaos, Solitons & Fractals, 9, 2023-2030.
[23]	El Naschie, M.S. (2007) On the Universality Class of All Universality Classes and E-Infinity Spacetime Physics. Chaos, Solitons & Fractals, 32, 927-936. http://dx.doi.org/10.1016/j.chaos.2006.08.017
[24]	El Naschie, M.S. (2014) Why E Is Not Equal to mc2. Journal of Modern Physics, 5, 743-750. http://dx.doi.org/10.4236/jmp.2014.59084
[25]	El Naschie, M.S. (2008) Average Exceptional Lie Group Hierarchy and High Energy Physics. American Institute of Physics Conference Proceedings, 1018, 15-20.
[26]	He, J.-H., Goldfain, E., Sigalotti, L.D. and Mejias, A. (2006) Beyond the 2006 Physics Nobel Prize for COBE: An Introduction to E-Infinity Spacetime Theory. China Science & Culture Publishing, Shanghai.
[27]	El Naschie, M.S. (2001) On a General Theory for Quantum Gravity. In: Diebner, H., Druckry, T. and Weibel, P., Eds., Science of the Interface, Genista Verlag, Tübingen, 52-57.
[28]	Duff, M. (1999) The World in Eleven Dimensions. IOP Publishing, Bristol.
[29]	Kaku, M. (2000) Strings, Conformal Fields and M-Theory. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-0503-6
[30]	Amendola, L. and Tsujikawa, S. (2010) Dark Energy: Theory and Observations. Cambridge University Press, Cambridge.
[31]	Rindler, W. (2004) Relativity (Special, General and Cosmological). Oxford University Press, Oxford.
[32]	Halvorson, H. (2011) Deep Beauty—Understanding the Quantum World through Mathematical Innovation. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511976971
[33]	Ho, M.-W. (2014) E-Infinity Spacetime, Quantum Paradoxes and Quantum Gravity. Journal of the Institute of Science in Society, 62, 40-43.
[34]	El Naschie, M.S. (1998) Superstrings, Knots and Noncommutative Geometry in E-Infinity Space. International Journal of Theoretical Physics, 37, 2935-2951. http://dx.doi.org/10.1023/A:1026679628582
[35]	El Naschie, M.S. (2006) Elementary Number Theory in Superstring Loop Quantum Mechanics, Twistors and E-Infinity High Energy Physics. Chaos, Solitons & Fractals, 27, 297-330. http://dx.doi.org/10.1016/j.chaos.2005.04.116
[36]	El Naschie, M.S. (2004) Quantum Gravity, Clifford Algebra, Fuzzy Set Theory and the Fundamental Constants of Nature. Chaos, Solitons & Fractals, 20, 297-330. http://dx.doi.org/10.1016/j.chaos.2003.09.029
[37]	El Naschie, M.S. (2009) The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646. http://dx.doi.org/10.1016/j.chaos.2008.09.059
[38]	El Naschie, M.S. (2009) Wild Topology, Hyperbolic Geometry and Fusion Algebra of High Energy Particle Physics. Chaos, Solitons & Fractals, 13, 1935-1945. http://dx.doi.org/10.1016/S0960-0779(01)00242-9
[39]	El Naschie, M.S. (2006) Hilbert, Fock and Cantorian Spaces in the Quantum Two-Slit Gedanken Experiment. Chaos, Solitons & Fractals, 27, 39-42. http://dx.doi.org/10.1016/j.chaos.2005.04.094
[40]	El Naschie, M.S. (1998) Penrose Universe and Cantorian Spacetime as a Model for Noncommutative Quantum Geometry. Chaos, Solitons & Fractals, 9, 931-933. http://dx.doi.org/10.1016/S0960-0779(98)00077-0
[41]	El Naschie, M.S. (2006) On an Eleven Dimensional E-Infinity Fractal Spacetime Theory. International Journal of Nonlinear Sciences & Numerical Simulation, 7, 407-409.
[42]	El Naschie, M.S. (2013) A Resolution of the Cosmic Dark Energy via Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26. http://dx.doi.org/10.4236/jqis.2013.31006
[43]	El Naschie, M.S. (2006) Topics in the Mathematical Physics of E-Infinity Theory. Chaos, Solitons & Fractals, 30, 656-663. http://dx.doi.org/10.1016/j.chaos.2006.04.043
[44]	El Naschie, M.S. (2007) From Symmetry to Particles. Chaos, Solitons & Fractals, 32, 427-430. http://dx.doi.org/10.1016/j.chaos.2006.09.016
[45]	Nottale, L. (2011) Scale Relativity and Fractal Space-Time. Imperial College Press, London.
[46]	El Naschie, M.S. (1994) Average Symmetry, Stability and Ergodicity of Multidimensional Cantor Sets. Il Nuovo Cimento B Series 11, 2, 149-157. http://dx.doi.org/10.1007/BF02727425
[47]	El Naschie, M.S. (1998) Fredholm Operator and the Wave-Particle Duality. Chaos, Solitons & Fractals, 9, 975-978. http://dx.doi.org/10.1016/S0960-0779(98)00076-9
[48]	El Naschie, M.S. (2008) Symmetry Group Prerequisite for E-Infinity High Energy Physics. Chaos, Solitons & Fractals, 35, 975-978.
[49]	El Naschie, M.S. (2007) Hilbert Space, Poincaré Dodecahedron and Golden Mean Transfiniteness. Chaos, Solitons & Fractals, 31, 787-793. http://dx.doi.org/10.1016/j.chaos.2006.06.003
[50]	Neuenschwander, D. (2011) Emmy Noether’s Wonderful Theorem. The Johns Hopkins University Press, Baltimore.
[51]	Balachandran, A., Kurkcuoglu, S. and Vaidya, S. (2007) Lectures on Fuzzy and Fuzzy SUSY Physics. World Scientific, Singapore.
[52]	Finkelstein, D.R. (1996) Quantum Relativity. A Synthesis of the Ideas of Einstein and Heisenberg. Springer, Berlin.
[53]	El Naschie, M.S. (2014) On a New Elementary Particle from the Disintegration of the Symplectic 'tHooft-Veltman-Wilson Fractal Spacetime. World Journal of Nuclear Science and Technology, 4, 216-221. http://dx.doi.org/10.4236/wjnst.2014.44027
[54]	El Naschie, M.S. (2014) From Modified Newtonian Gravity to Dark Energy via Quantum Entanglement. Journal of Applied Mathematics and Physics, 2, 803-806.
[55]	Tang, W., Li, Y., Kong, H.Y. and El Naschie, M.S. (2014) From Nonlocal Elasticity to Nonlocal Spacetime and Nanoscience. Bubbfil Nano Technology, 1, 3-12.
[56]	El Naschie, M.S. (2014) Cosmic Dark Energy Density from Classical Mechanics and Seemingly Redundant Riemannian Finitely Many Tensor Components of Einstein’s General Relativity. World Journal of Mechanics, 4, 153-156. http://dx.doi.org/10.4236/wjm.2014.46017
[57]	El Naschie, M.S. (2014) Compactified Dimensions as Produced by Quantum Entanglement, the Four Dimensionality of Einstein’s Smooth Spacetime and 'tHooft’s 4-ε Fractal Spacetime. American Journal of Astronomy & Astrophysics, 2, 34-37.
[58]	Auffray, J.-P. (2014) E-Infinity Dualities, Discontinuous Spacetimes, Xonic Quantum Physics and the Decisive Experiment.Journal of Modern Physics, 5, 1427-1436.
[59]	El Naschie, M.S. (2014) Electromagnetic—Pure Gravity Connection via Hardy’s Quantum Entanglement.Journal of Electromagnetic Analysis and Applications, 6, 233-237.
[60]	El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrodinger Quantum Wave.Journal of Modern Physics, 4, 591-596.
[61]	Wigner, E.P. (1960) The Unreasonable Effectiveness of Mathematics in Natural Science. Communications in Pure and Applied Mathematics, 13, 1-14. http://dx.doi.org/10.1002/cpa.3160130102
[62]	Changeux, J. and Connes, A. (1989) Conversation on Mind, Matter and Mathematics. Princeton University Press, Princeton.
[63]	Helal, M.A., Marek-Crnjac, L. and He, J.-H. (2013) The Three Page Guide to the Most Important Results of M. S. El Naschie’s Research in E-Infinity Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145. http://dx.doi.org/10.4236/ojm.2013.34020

From E = mc2 to E = mc2/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entanglement Origin

From E = mc2 to E = mc2/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entanglement Origin

From E = mc² to E = mc²/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entanglement Origin

 Download as PDF (Size:2647KB)  HTML   XML  PP. 284-291  

DOI: 10.4236/jqis.2014.44023    979 Downloads   1,444 Views  

Author(s)    Leave a comment

Mohamed S. El Naschie^*

Affiliation(s)

Department of Physics, University of Alexandria, Alexandria, Egypt.

ABSTRACT

Einstein’s energy mass formula is shown to consist of two basically quantum components E(O) = mc²/22 andE(D) = mc²(21/22). We give various arguments and derivations to expose the quantum entanglement physics residing inside a deceptively simple expression E = mc². The true surprising aspect of the present work is however the realization that all the involved “physics” in deriving the new quantum dissection of Einstein’s famous formula of special relativity is actually a pure mathematical necessity anchored in the phenomena of volume concentration of convex manifold in high dimensional quasi Banach spaces. Only an endophysical experiment encompassing the entire universe such as COBE, WMAP, Planck and supernova analysis could have discovered dark energy and our present dissection of Einstein’s marvelous formula.

KEYWORDS

Special Relativity, Varying Speed of Light, Hardy’s Quantum Entanglement, Dark Energy, Measure Concentration in Banach Space, ‘tHooft Fractal Spacetime, Witten Fractal M-Theory, E-Infinity Theory, Transfinite Cellular Automata, Golden Mean Computer, Endophysics, Finkelstein-Rössler-Primas Theory of Interface

Cite this paper

Naschie, M. (2014) From E = mc² to E = mc²/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entanglement Origin. Journal of Quantum Information Science, 4, 284-291. doi:10.4236/jqis.2014.44023.

References

[1]	Stachel, J. (1998) Einstein’s Miraculous Year. Princeton University Press, Princeton.
[2]	Eddington, A.S. (1987) Space, Time and Gravitation. Cambridge University Press, Cambridge.
[3]	Heisenberg, W. (1969) Der Teil und das Ganze. Piper-Verlag, Munich.
[4]	Crease, R.P. (2009) The Great Equation. Constable and Robinson, London.
[5]	Born, M. (1983) Physik in Wandelmeiner Zeit. Vieweg, Brauenschweig.
[6]	Hawking, S. (2007) The Essential Einstein. Penguin Books, London.
[7]	Pais, A. (2005) Subtle Is the Lord. Oxford University Press, Oxford.
[8]	Penrose, R. (2004) The Road to Reality. J. Cape, London.
[9]	Mageuijo, J. (2003) Faster than the Speed of Light. Heinemann, London.
[10]	Moffat, J. (2008) A Physicist Goes beyond Einstein. Smithsonian Books, New York.
[11]	Baryshev, Y. and Teerikorpi, P. (2002) Discovery of Cosmic Fractals. World Scientific, Singapore.
[12]	Carmeli, M. (2006) Cosmological Relativity. World Scientific, Singapore. http://dx.doi.org/10.1142/6275
[13]	Wesson, P.S. (2006) Five Dimensional Physics. World Scientific, Singapore.
[14]	Hawking, S. and Penrose, R. (1996) The Nature of Space and Time. Princeton University Press, Princeton.
[15]	Rindler, W. (2006) Relativity, Special, General and Cosmological. 2nd Edition, Oxford University Press, Oxford.
[16]	Zee, A. (1989) Einstein’s Universe. Oxford University Press, Oxford.
[17]	Ruiz-Lapuente, P. (2010) Dark Energy. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139193627
[18]	Ferreira, P.G. (2014) The Perfect Theory—A Century of Geniuses and the Battle over General Relativity. Little, Brown, London.
[19]	El Naschie, M.S. (2014) On a New Elementary Particle from the Disintegration of the Symplectic ‘t Hooft-Veltman-Wilson Fractal Spacetime. World Journal of Nuclear Science and Technology, 4, 216-221. http://dx.doi.org/10.4236/wjnst.2014.44027
[20]	Auffray, J.-P. (2014) E-Infinity Dualities, Discontinuous Spacetimes, Xonic Quantum Physics and the Decisive Experiment. Journal of Modern Physics, 5, 1427-1436. http://dx.doi.org/10.4236/jmp.2014.515144
[21]	El Naschie, M.S. (2014) Electromagnetic—Pure Gravity Connection via Hardy’s Quantum Entanglement.Journal of Electromagnetic Analysis and Applications, 6, 233-237. http://dx.doi.org/10.4236/jemaa.2014.69023
[22]	El Naschie, M.S. (2014) Why E Is Not Equal mc2. Journal of Modern Physics, 5, 743-750. http://dx.doi.org/10.4236/jmp.2014.59084
[23]	El Naschie, M.S., Marek-Crnjac, L., Helal, M.A. and He, J.-H. (2014) A Topological Magueijo-Smolin Varying Speed of Light Theory, the Accelerated Cosmic Expansion and the Dark Energy of Pure Gravity. Applied Mathematics, 5, 1780-1790. http://dx.doi.org/10.4236/am.2014.512171
[24]	El Naschie, M.S. (2014) Cosmic Dark Energy from ‘t Hooft’s Dimensional Regularization and Witten’s Topological Quantum Field Pure Gravity. Journal of Quantum Information Science, 4, 83-91. http://dx.doi.org/10.4236/jqis.2014.42008
[25]	El Naschie, M.S. (2013) A Resolution of Cosmic Dark Energy via a Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26. http://dx.doi.org/10.4236/jqis.2013.31006
[26]	El Naschie, M.S. (2013) A Unified Newtonian-Relativistic Quantum Resolution of the Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light. International Journal of Modern Nonlinear Theory and Application, 2, 43-54. http://dx.doi.org/10.4236/ijmnta.2013.21005
[27]	El Naschie, M.S. (2013) The Quantum Gravity Immirzi Parameter—A General Physical and Topological Interpretation. Gravity and Cosmology, 19, 151-153. http://dx.doi.org/10.1134/S0202289313030031
[28]	Helal, M.A., Marek-Crnjac, L. and He, J.-H. (2013) The Three Page Guide to the Most Important Results of M. S. El Naschie’s Research in E-Infinity Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145. http://dx.doi.org/10.4236/ojm.2013.34020
[29]	Marek-Crnjac, L. and He, J.-H. (2013) An Invitation to El Naschie’s Theory of Cantorian Space-Time and Dark Energy. International Journal of Astronomy and Astrophysics, 3, 464-471. http://dx.doi.org/10.4236/ijaa.2013.34053
[30]	He, J.-H. and Marek-Crnjac, L. (2013) Mohamed El Naschie’s Revision of Albert Einstein’s E = m0c2: A Definite Resolution of the Mystery of the Missing Dark Energy of the Cosmos. International Journal of Modern Nonlinear Theory and Application, 2, 55-59. http://dx.doi.org/10.4236/ijmnta.2013.21006
[31]	Wolf, P., Bize, S., Tobar, M.E., Chapelet, F., Clairon, A., Luiten, A.N. and Santarelli, G. (2005) Recent Experimental Tests of Special Relativity. http://arxiv.org/pdf/physics.class-ph/0506168.pdf
[32]	Reid, J.S. (2005) Why We Believe in Special Relativity: Experimental Support for Einstein’s Theory. In: Einstein 1905 Relativity, a Report of a Public Meeting Held in Aberdeen University, Scotland, 21 March 2005.
[33]	Pennicott, K. (2002) Cool Laser Puts Special Relativity to the Test. http://physicsworld.com/cws/article/news/2002/jan/08/cool- laser-puts-special-relativity-to-the-test
[34]	El Naschie, M.S. (2013) Scientific Homepage. http://mohamed-elnaschie.blogspot.co.uk
[35]	Guedon, O. (2014) Concentration Phenomena in High Dimensional Geometry. ESAIM Proceedings, 44, 47-60. http://dx.doi.org/10.1051/proc/201444002
[36]	El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
[37]	El Naschie, M.S., He, J.-H., Nada, S., Marek-Crnjac, L. and Helal, M.A. (2012) Golden Mean Computer for High Energy Physics. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 2, 80-93.
[38]	Bename, S. (2005) Scars of War Wounds of Peace: The Israeli-Arab Tragedy. Weidenfeld and Nicolson, London.
[39]	Rossler, O.E. and El Naschie, M.S. (1998) Interference Is Exophysically Absent. In: Rossler, O., Ed., Endophysics, World Scientific, Singapore, 159-160.
[40]	El Naschie, M.S. (2014) The Gap Labelling Integrated Density of States for a Quasi Crystal Universe Is Identical to the Observed 4.5 Percent Ordinary Energy Density of the Cosmos. Natural Science, 6, 1259-1265. http://dx.doi.org/10.4236/ns.2014.616115
[41]	El Naschie, M.S. (1996) Time Symmetry Breaking, Duality and Cantorian Spacetime. Chaos, Solitons & Fractals, 7, 499-518. http://dx.doi.org/10.1016/0960-0779(96)00007-0
[42]	El Naschie, M.S. (2001) On a General Theory of Quantum Gravity. In: Diebner, H., Druckery, T. and Weibel, P., Eds., Science of the Interface, Genistaverlag, Tübingen, 72-75.
[43]	Weinberg, S. (2001) Facing up. Harvard University Press, Cambridge.
[44]	Avnery, U. (1968) Israel ohneZionisten. Bertelmann Verlag, Gütersloh.
[45]	Stiglitz, J. (2008) The Three Trillion Dollar War—The True Cost of The Iraq Conflict. Allen Lan-Penguin, London.
[46]	Einstein, A. (1953) Mein Weltbild. Europa Verlag AG, Zurich.

From Kantian-Reinen Fernunft to the Real Dark Energy Density of the Cosmos via the Measure Concentration of Convex Geometry in Quasi Banach Spacetime

From Kantian-Reinen Fernunft to the Real Dark Energy Density of the Cosmos via the Measure Concentration of Convex Geometry in Quasi Banach Spacetime

From Kantian-Reinen Fernunft to the Real Dark Energy Density of the Cosmos via the Measure Concentration of Convex Geometry in Quasi Banach Spacetime

Mohamed S. El Naschie

Department of Physics, University of Alexandria, Alexandria, Egypt

Email: Chaossf@aol.com

Copyright © 2015 by author and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 5 February 2015; accepted 23 February 2015; published 26 February 2015

ABSTRACT

The paper argues strongly in favour of the opinion that Kantian pure reason could be implemented via pure mathematics to reveal a true deep aspect of the fundamental monads of the real physics of the cosmos. Thus using a remarkable pure mathematical-geometrical result stating that under certain conditions a manifold will have 96 percent of its volume concentrated near to its surface, we conclude that the 96 percent dark energy causing the edge of our universe to expand is a direct consequence of this pure geometrical result. From this viewpoint we could generalize our finding to mean that scientific philosophy is not only an important ingredient of human cultural existence but a real immensely important tool in analyzing the reality of the cosmos at the quantum level as well as its large scale structure.

Keywords:

Kant Critique of Pure Reason, Measure Concentration, Convex Geometry, Dvoretzky’s Theorem, Very High Space Dimensionality, Banach Spaces, E-Infinity Spectra, Dark Energy, E Equals mc² Divided by 22, Scientific Philosophy, Pure Mathematics in Physics, Einstein Relativity, Quantum Gravity

1. Introduction

The present work is devoted mainly to clarifying problems connected to Einstein’s relativity(Rindler, 2004; Okun, 2009; Helal et al., 2013; He & Marek-Crnjac, 2013; Helal, Marek-Crnjac, & He, 2013.; Auffray, 2014; El Naschie, 2011, 2013a-k, 2014a-m) and the missing dark energy of the cosmos (Auffray, 2014; El Naschie, 2011, 2012a-2, 20131-k, 2014a-m; He, 2013a; He & Marek-Crnjac, 2013b; Marek-Crnjac, 2013a; Marek-Crnjac & El Naschie, 2013b; Marek-Crnjac & He, 2013c; Marek-Crnjac, El Naschie, & He, 2013d; Tang et al., 2014) as well as quantum gravity and high energy physics (El Naschie, 2011-2014; Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013; He & El Naschie, 2012; He 2013a; He & Marek-Crnjac, 2013b; He, 2014; Connes, 1994; Krantz & Parks, 2008) using pure mathematics (Kant, 1974; Baumgartner, 1988; Sartre, 2004, 2012; Reichenbach, 1951; Ayer, 1954; El Naschie, 1994) . Taking a bird’s eye view of things it is reasonably safe, even for a theoretical physicist and engineering scientist like the present author, to state that almost the entire modern philosophical framework of our present society is shaped by and stands on Kant’s critique of pure reason as well as his critique of practical reason (Kant, 1974; Baumgartner, 1988) . From there German idealism invaded the intellectual foundations of not only European civilization but the entire world which culminated in the work of F. Hegel giving rise to Marxism and existentialism. In fact the hero of the present author in his youth and early life was J. P. Sartre (Sartre, 2004, 2012) . In particular Sartre’s critique of the dialectic reason and in no minor measure his main monumental work, being and nothingness influenced the writer to discover the zero set as the quantum particle and the empty set as the quantum wave and introduced Mandelbrot’s notion of the degrees of emptiness of an empty set to the transfinite set theory used by him and the E-infinity school of high energy physics (El Naschie 1994, 2014a-m; He & El Naschie, 2012) . Looking back without any Osbornian anger, it is clear to the author that he believed rather strongly that philosophy has a real, indispensible role in exact science, a belief many disputed in physics but is held highly by many pure mathematicians, notably G. Cantor and in modern times, also by leading mathematicians working also in physics such as Field Medalist (A. Connes, 1994) . This was all fine and good and things remained as they are until the present ideas constituting the main body of the present work dawned on the author. A seemingly harmless theorem in the mathematics of convex geometry in very high dimensions related to Banach spaces states that for manifolds of this mould, 96 percent of the measure volume will be concentrated near to the surface of the manifold (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013) . Suddenly a mental analogue of atomic chain reaction was triggered in the mind of the author and it became evident for him that this theorem is the counter part of Kant’s pure reason applied to the “experimentally” discovered mystery of the “missing” dark energy of the universe (El Naschie, 2012a-c, 20131-k, 2014a-m; He 2013a; He & Marek-Crnjac, 2013b; Marek-Crnjac, 2013a; Marek-Crnjac & El Naschie, 2013b; Marek-Crnjac & He, 2013c; Marek-Crnjac et al., 2013d) . This would, and the present author believe it is a clear cut generic and fundamental example for the power of scientific philosophical thinking in reaching in a direct way a resolution for fundamental problems in quantum physics and cosmology. To try to persuade the reader that this is the case requires some knowledge of math and physics but none of it is so hard or extremely specialized that the non-specialist cannot follow as we hope to show next.

2. General Background Information

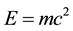Einstein’s most famous formula states the equivalence of matter and energy and relates them via the constant speed of light in the jewel of special relativity  where 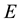 is the energy, 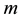is the mass and  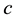is the speed of light (Rindler, 2004; Okun, 2009; Helal et al., 2013) . Intensive effort motivated by the unexpected discovery of the accelerated expansion of the cosmos and the related problem of the dark matter and dark energy 95% density deficit revealed that Einstein’s energy “density” equation is the sum of two parts (Auffray, 2014) . The first is a measurable ordinary energy  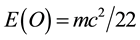and the second which cannot be measured in any conventional way is the dark energy density  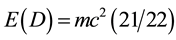so that at the end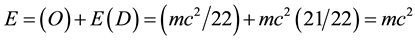. To arrive at this result two main groups of methods were employed (Helal et al., 2013; Auffray, 2014; El Naschie, 2011, 2012a-c, 2013a-k, 2014a-m; He, 2013a; He & Marek-Crnjac, 2013b; Marek-Crnjac, 2013a; Marek-Crnjac & El Naschie, 2013b; Marek-Crnjac & He, 2013c; Marek-Crnjac et al., 2013d; Tang et al., 2014) . The first may be loosely described as mainly physical based on the structure of the standard model of elementary high energy particles while the second may be equally loosely described as largely mathematical starting from Cantor transfinite set theory.

In the present paper by contrast we tackle the problem afresh using a purely topological-geometrical methodology based on some remarkable mathematical results from the modern theory of high dimensional convex geometry and the associated phenomenon of concentration of measure studied initially in Banach spaces and then lead to Dvoretzky’s theorem and the subsequent relevant research (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013) .

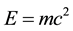We stress again that the final result is a complete confirmation of the dissection of  into 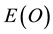 of the quantum particle and  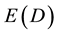of the quantum wave in addition to being a deep insight into the relation between physics, geometry and algebra as well as the unity of classical and quantum mechanics (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013; Connes, 1994; Krantz & Parks, 2008) . Our main message in this paper is that real fundamental, physical and cosmological facts could be found using pure reason (Kant, 1974; Baumgartner, 1988; Sartre, 2004, 2012; Reichenbach, 1951; Ayer, 1954; El Naschie, 1994) .

3. Further Background Information and Preliminary Considerations

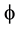Cantorian spacetime is a monadic space (He, 2012) in a sense akin to that of K-theory, E-infinity rings and n- category theory. The building blocks of this space are zero sets of a Hausdorff dimension  embedded into empty sets of a Hausdorff  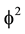which are distributed in a uniform randomness to form via an infinite number of unions and intersections a hierarchical-infinite dimensional Cantor set. This Suslin-like operation (Krantz & Parks, 2008) entails few fundamental equations which determine all what is required to deduce various vital invariant properties of this space which we use to mimic our own physical macro and micro quantum spacetime. Based on the above we were able to show in the last four years beyond reasonable doubt that the jewel of special relativity, i.e. 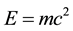is in fact the sum of two partial equations. As mentioned earlier on in the introduction, the first part  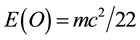gives us the real measurable energy density which is due to the particle side of quantum mechanics as modelled by the zero set in Kaluza-Klein five dimensional spacetime. The second part on the other hand is the dark energy which cannot be measured in the ordinary way  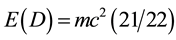and which is due to the wave nature of the quantum particle-wave duality as modelled by the empty set in the same K-K spacetime. A trivial computation shows then that 1/22 = 4.5% and 21/22 = 95.5% of Einstein’s total energy density in complete agreement with all modern cosmological measurements. Again in the last four years numerous derivations of the preceding dissection of Einstein’s basic energy-mass relation was given by the author and his collaborators using a variety of physical and algebraic derivation and all leading to the same fundamental conclusion.

The present work is not intended to review or discuss in details past derivations but is mainly concerned with giving a new purely geometrical derivation showing that the so called missing 95.5% dark energy is a well established geometrical phenomena completely understood since many years in the mathematical literature without drawing or suspecting any physical conclusion or relation to high energy quantum physics or cosmology (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013) . We are talking here about the phenomenon of measure concentration of convex geometry with high dimensionality which is an off spring of research works on Banach spaces (El Naschie, 2012a-c) . The next section is mainly concerned with outlining and explaining this fascinating new connection between pure geometry, quantum physics and cosmology as well as how classical mechanics arise from the deeper mechanics of the quantum and the even deeper mathematics of transfinite set theory and infinite dimensional Banach spaces.

4. Cantorian Spacetime as a Convex Geometry in Very High Dimensions

4.1. Short Review of the Relevant Results in Convex Geometry

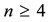The aim of this minimalistic section is to show the failure of our low dimensionality intuition when dealing with geometrical objects of higher dimensionality which start in earnest with  (El Naschie, 1997, 1999) . Similar ideas were discussed by the present author many years ago while attempting to connect string theory and the geometry of spacetime with sphere backing and chess board tiling. The present fundamental example goes in the same main direction and even beyond to the degree that it becomes of fundamental importance in the cosmology of dark energy. To start let us calculate the  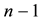dimensional slice of a unit ball. The relatively elementary consideration involving the use of the stirling formula leads to an accurate approximation of the volume of the smaller slice (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013)

, (1)

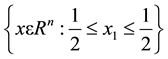where  fixes the width of parallel slices. That way we can conclude that the volume “mass”

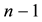volume “mass” distribution is Gaussian and for a fixed slab width almost 95.5% of the mass lies in this slice (Ball, 1991) . Now as hinted at earlier, our intuition could lead us to wrongly think that this 95.5% measure concentration is located in dimension  at the centre of the 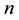-dimensional space. The mathematical-geome- trical truth however is exactly the opposite and careful consideration reveals that for large  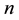the measure concentration is asymptotically near to the surface (Ball, 1991) . For  the 95.5% is for all practical reasons the surface itself. The mathematical literature is in the meantime abounds with various extensions of this remarkable result which is based on A. Dvoretzky’s theorem and the work of V. Milman and its mathematical-geometrical ramifications (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013) . In the present work however our evident interest is clearly in the obvious relevance of the above conclusion to dark energy cosmology. We start by showing the almost one to one correspondence of the above with the Cantorian-fractal holographic boundary of E-infinity spacetime and its dark energy content.

4.2. The Measure Concentration of E-Infinity Spacetime as an Explanation for Dark Energy

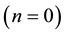As mentioned earlier on in the introduction, the building blocks of E-infinity Cantorian spacetime are zero sets embedded into an empty set as their surface or cobordism. Since the zero set  has a Hausdorff dimension  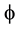and the empty set  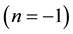has a Hausdorff dimension  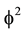then in  Kaluza-Klein spacetime the unit volumetric measure would be the average of intersectional  zero set volume 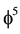 nd the additive  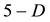empty set volume  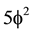here we interprete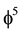d  and 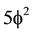 s a Hausdorff volume or topological probability as an extension of the classical notion of geometrical probability (Helal et al., 2013; Marek-Crnjac, 2013a; Marek-Crnjac & El Naschie, 2013b; Marek-Crnjac & He, 2013c; Marek-Crnjac et al., 2013d; Auffray, 2014; El Naschie, 2004, 2009) . Consequently the average volume is simply (Connes, 1994)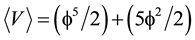

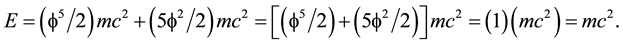
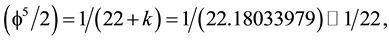
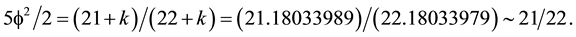
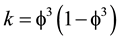. (2)

The corresponding average energy is therefore nothing else but Einstein’s celebrated formula [28]

(3)

From [28]

(4)

and

(5)

where  is the topological mass of ‘tHooft’s renormalon which could be thought of as made of two entangleon  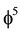particles because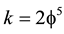, our main result follows, namely that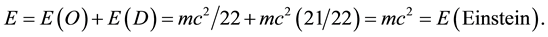

(6)

So far we have looked at a single monadic building block of our space (He, 2012). However due to self similarity we expect the above relation to hold true on all scales. To show that this expectation is correct and leads to our fundamental conclusion about the measure concentration, we reason as follows:

Our E-infinity spae is infinite dimensional, however it has a finite expectation value of 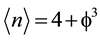 and 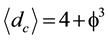 for its topological and Hausdorff dimension apart of the Menger-Urysohn topological dimension of exactly 4 (El Naschie, 2004, 2009) . Thus although infinite dimensional, because of its hierarchal geometry reflected in its Suslin expansion (Krantz & Parks, 2008)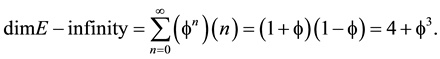

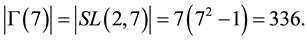
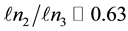(7)

it is still compact with a boundary at infinity. This shows up clearly in the hyperbolic projection of E-infinity space which manifests itself as a modular fractal space of the Klein-Penrose type as explained in great detail in previous older and more recent publications. Now our result follows because in the Poincare-Beltrami projection we have at the center about 336 degrees of freedom corresponding to the internal dimension of the original Klein modular space

(8)

This represents the holographic boundary without the “compactified” edge. At this edge however, which is located at infinity, we have infinitely more degrees of freedom. Thus although the edge seems to us from the middle to be infinitely think it is really where the bulk of absolute measure is located, namely the 95.5%. For us low dimensional creatures, the situation may strike us as paradoxical especially when we are making measurements of the total energy density of the cosmos. In this sense the COBE, WMAP and Planck measurement makes absolute sense when we realize that this 95.5% is related to the quantum wave of the universe which collapses on measurement and cannot be detected but can be indirectly inferred from cosmological observations extended to the edge of the universe.

5. Discussion

The quantum wave and wave collapse may be a familiar face of the quantum world but this does not change its deep status as the greatest puzzle in physics. How could something which has no energy, no matter and no momentum have such a crucial effect on the motion of quantum objects. Suddenly however cosmology started becoming equally puzzling, if not more puzzling, with the discovery of a type of energy which may be the possible cause behind the accelerated cosmic expansion of the universe although it is de facto not there because it cannot be measured and if we try very hard, we find only 4.5% ordinary energy and ordinary matter leaving the 95.5% shrouded in mystery. These things which are there but are really not there remind anyone working in deterministic chaos, nonlinear dynamics and fractals with the paradoxical nature of a Cantor set (El Naschie, 2004, 2009) . These transfinite sets possess no measure, being of measure zero which means no length at all and consequently “physically” not there. However they do have a substantial Hausdorff dimension, namely  for the original Cantor set and 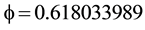for a uniformally random Mauldin-Williams Cantor set. Now we ask ourselves how did we succeed in applying an Occam razon magnum to these three paradoxical factors? The short answer is by reducing dark energy to the non-ordinary energy of the quantum wave and the quantum wave to an empty set dimension  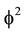which happens to be the surface of the zero set quantum particle with a Hausdorff dimension  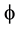That way we seem to have eliminated the problem by illuminating it via the light of fractal Cantorian geometry and transfinite set theory as well as the associated E-infinity algebra of the highly structured golden mean ring which can deal with the most complex computation with unheard of simplicity. Thus the present work shows a clear and profound example of how pure reason and pure mathematics guided by scientific philosophy and accurate measurements and observations can lead in a simple way to profound information about the real world.

6. Conclusion

The present work demonstrates that at the most fundamental quantum level the universe is best studied by pure reason and pure mathematics. We cannot experimentally probe either zero and nothingness or the uncountably infinite. However the present work clearly shows that the disection of Einstein’s energy density into two parts is a completely natural consequence of a very high dimensional geometry and its associated measure concentration which results in almost 96% of the volume being located near to the surface of the concerned manifold (Ball, 1991; Guedon, 2013) as well as modelling the quantum particle with a five dimensional zero set and modelling the quantum wave with a five dimensional empty set (El Naschie, 2013a-k) . Applied to our cosmos as modelled by E-infinity Cantorian spacetime manifold, the missing dark energy becomes a natural consequence of the geometry and topology of E-infinity. Together with our anticlastic, anti-curvature and antigravity explanation of real material-like spacetime (El Naschie, 2014a-m) , dark energy and accelerated cosmic expansion find in the above a rational mathematical-geometrical and consequently physical explanation.

References

1.  Auffray, J.-P. (2014). E-Infinity Dualities, Discontinuous Spacetimes, Xonic Quantum Physics and the Decisive Experiment. Journal of Modern Physics, 5, 1427-1436.http://dx.doi.org/10.4236/jmp.2014.515144
2. Ayer, A. J. (Ed.) (1954). Logical Positivism. Westport: Greenwood Press.http://dx.doi.org/10.1112/jlms/s2-44.2.351
3.  Ball, K. M. (1991). Volume Ratios and a Reverse Isoperimetric Inequality. Journal of London Mathematical Society, 44, 351-359.
4. Baumgartner, H. M. (1988). Kants Kritik der Reinen Vernunft. Man and World, 21, 241-259. http://dx.doi.org/10.1007/BF01252320
5. Connes, A. (1994). Noncommutative Geometry. San Diego: Academic Press.
6. El Naschie, M. S. (1997). Introduction to Nonlinear Dynamics, General Relativity and the Quantum―The Uneven Flow of Fractal Time. Chaos, Solitons & Fractals, 8, vii-x.http://dx.doi.org/10.1016/S0960-0779(97)88695-X
7. El Naschie, M. S. (1999). Hyper-Dimensional Geometry and the Nature of Physical Spacetime. Chaos, Solitons & Fractals, 10, 155-158. http://dx.doi.org/10.1016/S0960-0779(98)00235-5
8. El Naschie, M. S. (2004). A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236.http://dx.doi.org/10.1016/S0960-0779(03)00278-9
9. El Naschie, M. S. (2009). The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646.http://dx.doi.org/10.1016/j.chaos.2008.09.059
10. El Naschie, M. S. (2011). Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53.http://dx.doi.org/10.4236/jqis.2011.12007
11. El Naschie, M. S. (2012a). The Minus One Connection of Relativity, Quantum Mechanics and Set Theory. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 2, 131-134.
12. El Naschie, M. S. (2012b). Revising Einstein’s E = mc²; A Theoretical Resolution of the Mystery of Dark Energy. Proceedings of the Fourth Arab International Conference in Physics and Material Science, Alexandria, 1-3 October 2012.
13. El Naschie, M. S. (2012c). Towards a General Transfinite Set Theory for Quantum Mechanics. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 2, 135-142.
14. El Naschie, M. S. (2013a). A Resolution of Cosmic Dark Energy via a Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26.http://dx.doi.org/10.4236/jqis.2013.31006
15. El Naschie, M. S. (2013b). A Rindler-KAM Spacetime Geometry and Scaling the Planck Scale Solves Quantum Relativity and Explains Dark Energy. International Journal of Astronomy and Astrophysics, 3, 483-493. http://dx.doi.org/10.4236/ijaa.2013.34056
16. El Naschie, M. S. (2013c). A Unified Newtonian-Relativistic Quantum Resolution of the Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light. International Journal of Modern Nonlinear Theory and Application, 2, 43-54.http://dx.doi.org/10.4236/ijmnta.2013.21005
17. El Naschie, M. S. (2013d). Determining the Missing Dark Energy Density of the Cosmos from a Light Cone Exact Relativistic Analysis. Journal of Physics, 2, 19-25.
18. El Naschie, M. S. (2013e). Experimentally Based Theoretical Arguments that Unruh’s Temperature, Hawking’s Vacuum Fluctuation and Rindler’s Wedge Are Physically Real. American Journal of Modern Physics, 2, 357-361.http://dx.doi.org/10.11648/j.ajmp.20130206.23
19. El Naschie, M. S. (2013f). From Yang-Mills Photon in Curved Spacetime to Dark Energy Density. Journal of Quantum Information Science, 3, 121-126.http://dx.doi.org/10.4236/jqis.2013.34016
20. El Naschie, M. S. (2013g). The Hyperbolic Extension of Sigalotti-Hendi-Sharifzadeh’s Golden Triangle of Special Theory of Relativity and the Nature of Dark Energy. Journal of Modern Physics, 4, 354-356. http://dx.doi.org/10.4236/jmp.2013.43049
21. El Naschie, M. S. (2013h). The Quantum Entanglement behind the Missing Dark Energy. Journal of Modern Physics and Applications, 2, 88-96.
22. El Naschie, M. S. (2013i). The Quantum Gravity Immirzi Parameter―A General Physical and Topological Interpretation. Gravitation and Cosmology, 19, 151-155.http://dx.doi.org/10.1134/S0202289313030031
23. El Naschie, M. S. (2013j). Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrodinger Quantum Wave. Journal of Modern Physics, 4, 591-596. http://dx.doi.org/10.4236/jmp.2013.45084
24. El Naschie, M. S. (2013k). What Is the Missing Dark Energy in a Nutshell and the Hawking-Hartle Quantum Wave Collapse. International Journal of Astronomy and Astrophysics, 3, 205-211. http://dx.doi.org/10.4236/ijaa.2013.33024
25. El Naschie, M. S. (2014a). Calculating the Exact Experimental Density of the Dark Energy in the Cosmos Assuming a Fractal Speed of Light. International Journal of Modern Nonlinear Theory and Application, 3, 1-5. http://dx.doi.org/10.4236/ijmnta.2014.31001
26. El Naschie, M. S. (2014b). Cosmic Dark Energy from ‘t Hooft’s Dimensional Regularization and Witten’s Topological Quantum Field Pure Gravity. Journal of Quantum Information Science, 4, 83-91. http://dx.doi.org/10.4236/jqis.2014.42008
27.  El Naschie, M . S. (2014c). Cosserat-Cartan Modification of Einstein-Riemann Relativity and Cosmic Dark Energy Density. American Journal of Modern Physics, 3, 82-87.http://dx.doi.org/10.11648/j.ajmp.20140302.17
28. El Naschie, M. S. (2014d). Dark Energy and Its Cosmic Density from Einstein’s Relativity and Gauge Fields Renormalization Leading to the Possibility of a New ‘t Hooft Quasi Particle. The Open Journal of Astronomy, in press.
29. El Naschie, M. S. (2014e). Dark Energy via Quantum Field Theory in Curved Spacetime. Journal of Modern Physics and Applications, 2, 1-7.
30. El Naschie, M. S. (2014f). Deriving E = mc²/22 of Einstein’s Ordinary Quantum Relativity Energy Density from the Lie Symmetry Group SO(10) of Grand Unification of All Fundamental Forces and without Quantum Mechanics. American Journal of Mechanics and Applications, 2, 6-9.
31. El Naschie, M. S. (2014g). From Modified Newtonian Gravity to Dark Energy via Quantum Entanglement. Journal of Applied Mathematics and Physics, 2, 803-806.
32. El Naschie, M. S. (2014h). Hardy’s Entanglement as the Ultimate Explanation for the Observed Cosmic Dark Energy and Accelerated Expansion. International Journal of High Energy Physics, 1, 13-17.
33. El Naschie, M. S. (2014i). Logarithmic Running of ‘t Hooft-Polyakov Monopole to Dark Energy. International Journal of High Energy Physics, 1, 1-5.
34. El Naschie, M. S. (2014j). Pinched Material Einstein Space-Time Produces Accelerated Cosmic Expansion. International Journal of Astronomy and Astrophysics, 4, 80-90.http://dx.doi.org/10.4236/ijaa.2014.41009
35. El Naschie, M. S. (2014k). Rindler Space Derivation of Dark Energy. Journal of Modern Physics and Applications, 6, 1-10.
36. El Naschie, M. S. (2014l). The Meta Energy of Dark Energy. Open Journal of Philosophy, 4, 157-159. http://dx.doi.org/10.4236/ojpp.2014.42022
37. El Naschie, M. S. (2014m). Why E Is Not Equal to mc². Journal of Modern Physics, 5, 743-750. http://dx.doi.org/10.4236/jmp.2014.59084
38. El Naschie, M. S., & Helal, A. (2013). Dark Energy Explained via the Hawking-Hartle Quantum Wave and the Topology of Cosmic Crystallography. International Journal of Astronomy and Astrophysics, 3, 318-343. http://dx.doi.org/10.4236/ijaa.2013.33037
39. El Naschie, M. S., & Marek-Crnjac, L. (2012). Deriving the Exact Percentage of Dark Energy Using a Transfinite Version of Nottale’s Scale Relativity. International Journal of Modern Nonlinear Theory and Application, 1, 118-124.http://dx.doi.org/10.4236/ijmnta.2012.14018
40. El Naschie, M. S., He, J. H., Marek-Crnjac, L., & Helal, A. (2014). A Topological Magueijo-Smolin Varying Speed of Light Theory, the Accelerated Cosmic Expansion and the Dark Energy of Pure Gravity. Applied Mathematics, 5, 1780-1790.http://dx.doi.org/10.4236/am.2014.512171
41. El Naschie, M. S., He, J. H., Nada, S., Marek-Crnjac, L., & Helal, M. A. (2012a). Golden Mean Computer for High Energy Physics. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 2, 80-92.
42. El Naschie, M. S., Olsen, S., He, J. H., Nada, S., Marek-Crnjac, L., & Helal, A. (2012b). On the Need for Fractal Logic in High Energy Quantum Physics. International Journal of Modern Nonlinear Theory and Application, 1, 84-92.http://dx.doi.org/10.4236/ijmnta.2012.13012
43. El Naschie, M. S. (1994) On Certain Empty Cantor Sets and Their Dimensions. Chaos, Solitons & Fractals, 4, 293-296. http://dx.doi.org/10.1016/0960-0779(94)90152-X
44. Guedon, O. (2013). Concentration Phenomena in High Dimensional Geometry. arXiv:1310.1204.
45. He, J. H. (2014). A Tutorial Review on Fractal Spacetime and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718.http://dx.doi.org/10.1007/s10773-014-2123-8
46. He, J. H. (Guest Editor) (2013). Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics.. Special Issue on Recent Developments on Dark Energy and Dark Matter, 1-62.
47. He, J. H., & El Naschie, M. S. (2012). On the Monadic Nature of Quantum Gravity as a Highly Structured Golden Ring, Spaces and Spectra. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 2, 94-98.
48. He, J. H., & Marek-Crnjac, L. (2013). Mohamed El Naschie’s Revision of Albert Einstein’s E = mc²: A Definite Resolution of the Mystery of the Missing Dark Energy of the Cosmos. International Journal of Modern Nonlinear Theory and Application, 2, 55-59.http://dx.doi.org/10.4236/ijmnta.2013.21006
49. Helal, M. A., Marek-Crnjac, L., & He, J. H. (2013). The Three Page Guide to the Most Important Results of M. S. El Naschie’s Research in E-Infinity Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145.
50.  Kant, I. (1974). Kritik der reinen Vernunft. 2 Volum, Frankfurt/M.61982.
51. Kasin, B. S. (1977). The Width of Certain Finite-Dimensional Sets and Classes of Smooth Functions. IZV. Akad. Nauk. SSSR. Ser. Mat., 41, 334-351. (In Russian)
52. Krantz, S. G., & Parks, H. R. (2008). Geometric Integration Theory. Boston, MA: Birkhauser. http://dx.doi.org/10.1007/978-0-8176-4679-0
53. Marek-Crnjac, L. (2013). Modification of Einstein’s E = mc² to E = (1/22)mc². American Journal of Modern Physics, 2, 255-263. http://dx.doi.org/10.11648/j.ajmp.20130205.14
54. Marek-Crnjac, L., & El Naschie, M. S. (2013). Quantum Gravity and Dark Energy Using Fractal Planck Scaling. Journal of Modern Physics, 4, 31-38.http://dx.doi.org/10.4236/jmp.2013.411A1005
55. Marek-Crnjac, L., & He, J. H. (2013). An Invitation to El Naschie’s Theory of Cantorian Space-Time and Dark Energy. International Journal of Astronomy and Astrophysics, 3, 464-471. http://dx.doi.org/10.4236/ijaa.2013.34053
56. Marek-Crnjac, L., El Naschie, M. S., & He, J. H. (2013). Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology. International Journal of Modern Nonlinear Theory and Application, 2, 78-88. http://dx.doi.org/10.4236/ijmnta.2013.21A010
57. Okun, L. B. (2009). Energy and Mass in Relativity Theory. Singapore City: World Scientific.
58. Pisier, G. (1989). The Volume of Convex Bodies and Banach Space Geometry. Tracts in Math 94, Cambridge: Cambridge University Press.http://dx.doi.org/10.1017/CBO9780511662454
59. Reichenbach, H. (1951). The Rise of Scientific Philosophy. Oakland, CA: University of California Press.
60. Rindler, W. (2004). Relativity (Special, General and Cosmological). Oxford: Oxford University Press.
61. Sartre, J. P. (2004). Critique of Dialectic Reason. London/New York: Verso.
62. Sartre, J. P. (2012). Being and Nothingness. New York: Open Road Media.
63. Tang, W., Li, Y., Kong, H. Y., & El Naschie, M. S. (2014). From Nonlocal Elasticity to Nonlocal Spacetime and Nano Science. Bubbfil Nanotechnology, 1, 3-12.